Classification with a Neural Network
Neural networks are advanced computational models that mimic the human brain's structure, enabling them to capture and model complex, non-linear relationships between inputs and outputs. They consist of layers of perceptrons (neurons) that process inputs through weighted connections.
Structure of Neural Networks
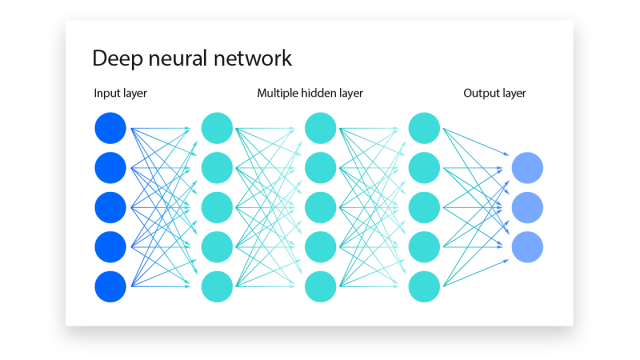
What is a Neural Network? | IBM
- Input Layer: The first layer that receives the input.
- Hidden Layers: One or more layers that process the inputs from the previous layer and pass the output to the next layer. Each neuron in a hidden layer transforms the inputs with a weighted sum followed by a non-linear activation function.
- Output Layer: The final layer that produces the network's output.
Mathematical Model
Notations
- : Weight from neuron in the previous layer to neuron in the current layer.
- : Bias term for neuron .
- : Weighted sum of inputs for neuron .
- : Activation function applied to , often a sigmoid function.
- : Output of neuron after applying the activation function.
- : Loss function measuring the prediction error, where is the actual target and is the predicted output.
Forward Propagation
- Input to Hidden Layer: Calculates the weighted sum of inputs and applies the activation function to each neuron in the hidden layer.
- Hidden to Output Layer: Processes the outputs from the hidden layer to produce the final prediction.
Backpropagation and Gradient Descent
Derivatives for Gradient Descent
The partial derivative of the loss function with respect to a weight is given by the chain rule:
- : Derivative of the weighted sum with respect to the weight, typically the input for the corresponding weight.
- : Derivative of the activation function.
The weights are updated using the rule:
where is the learning rate.
Training Multi-Layer Networks
For networks with multiple hidden layers, the notation includes superscripts to denote layer numbers (, , etc.). The training process involves a forward pass to compute activations and a backward pass (backpropagation) to compute gradients and update weights and biases using gradient descent.
Loss Function and Derivatives
The loss function quantifies the difference between actual and predicted outputs. The gradient of the loss function with respect to weights and biases (, ) guides the updates during training.
Chain Rule Application
The chain rule is applied to compute derivatives across multiple layers, enabling the calculation of how changes in weights and biases affect the overall loss.
Updating Weights and Biases
Weight and Bias Update Formula
- For weights:
- For biases:
Simplification for Biases
The update process for biases is simplified, as they directly affect the neuron's output without being multiplied by an input value.
Conclusion
Neural networks model complex patterns through their layered structure and nonlinear input transformations. Training involves adjusting weights and biases to minimize loss, a process facilitated by backpropagation and gradient descent.